On Optimisation in Matrix Completion

Statisticians get their first taste of optimisation when they learn about penalised linear regression:

It turns out that there's an equivalent formulation (as a constrained minimisation) that provides a little more intuition:

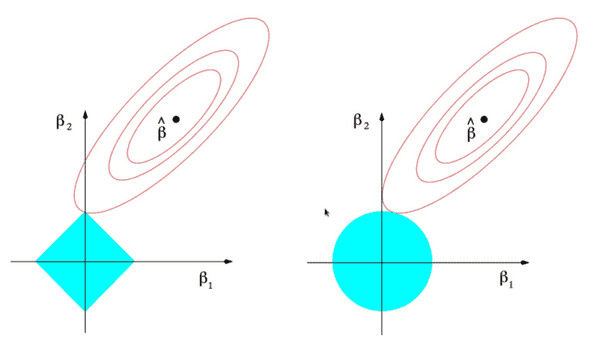
where there is a one-to-one relation between $\lambda$ and $s$. This different view provides a geometric interpretation: depending on the geometry induced by the $l_p$ ball that is the constraint set, you're going to get different kinds of solutions.

Note that the above equivalence is exact only when the loss and the penalty are both convex. In the matrix completion setting ([[penalty-project]]), this is no longer the case.

The (classical) convex program (Candes & Recht, 2009)^{Candes:2009kj} is given by:

where setting $\epsilon = 0$ reduces to the noise-less setting. The more recent development using a penalised linear model is given by:

Since they're both convex, you have equivalence just like for the Lasso.¹

Non-Convex

What happens when we move to non-convex penalties though? Then, I think what you have is a duality gap (I could be wrong). If we use our penalty $\frac{\|{W}_{\star}}{\|{W}_{F}}$, then these two views are no longer equivalent. And here I think actually going back to the penalised loss function gives better results. For one thing, it's no longer a convex program, amenable to simple solvers.