Exponential Learning Rates

via blog and (Li & Arora, 2019)^Li:2019tn

Two key properties of SOTA nets: normalisation of parameters within layers (Batch Norm); and weight decay (i.e $l_2$ regulariser, [[explicit-regularization]]). For some reason I never thought of [[batch-norm]] as falling in the category of normalisations (see Effectiveness of Normalised Quantities).

It has been noted that BN + WD can be viewed as increasing the learning rate (LR).

When combined with BN, this implies strange dynamics in parameter space, and the experimental papers (van Laarhoven, 2017, Hoffer et al., 2018a and Zhang et al., 2019), noticed that combining BN and weight decay can be viewed as increasing the LR.

What they show is the following:

(Informal Theorem) Weight Decay + Constant LR + BN + Momentum is equivalent (in function space) to ExpLR + BN + Momentum

The proof holds for any loss function satisfying scale invariance:

Here's an important Lemma:

Lemma: A scale-invariant loss $L$ satisfies:

Proof: Taking derivatives of $L(c \cdot \theta) = L(\theta)$ wrt $c$, and then setting $c=1$ gives the first result. Taking derivatives wrt $\theta$ gives the second result.

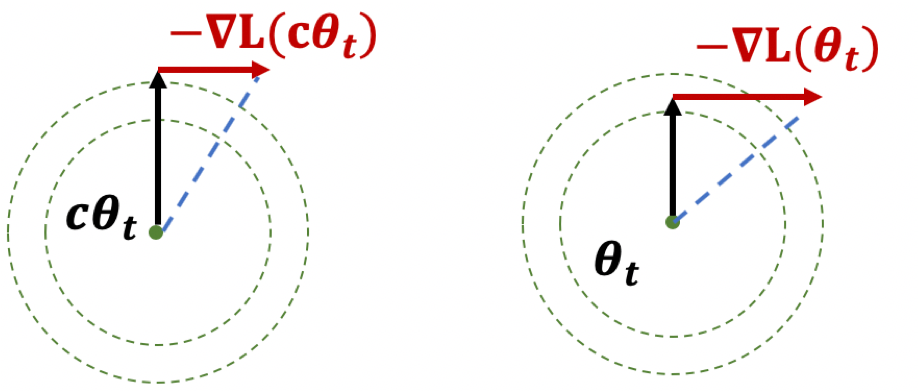
The first result, if you think of it geometrically, ensures that $|\theta|$ is increasing. The second result shows that while the loss is scale-invariant, the gradients have a sort of corrective factor such that larger parameters have smaller gradients.

Thoughts

The paper itself is more interested in learning rates. What I think is interesting here is the preoccupation with scale-invariance. There seems to be something self-correcting about it that makes it ideal for neural network training. Also, I wonder if there is any way to use the above scale-invariance facts in our proofs.

They also deal with learning rates, except that the rates themselves are uniform across all parameters, making it much easier to analyze – unlike Adam where you have adaptivity.