Calculus For Brain Computation

src: video, pdf

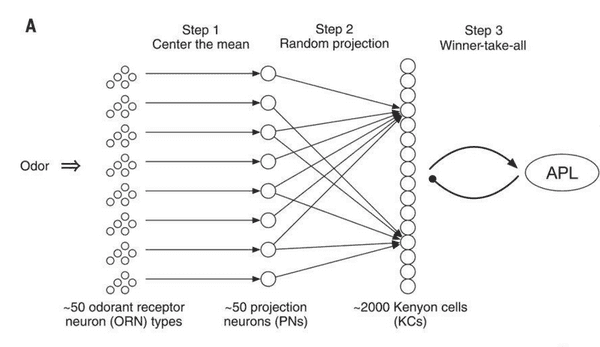
• olfactory intelligence: centring -> random projection (50 to 2000) -> sparsification
• $\mathbb{R}^{50} \to \mathbb{R}^{2000} \to \{0,1\}^{2000}$ (sparsity at the 10% level, thresholding the top).

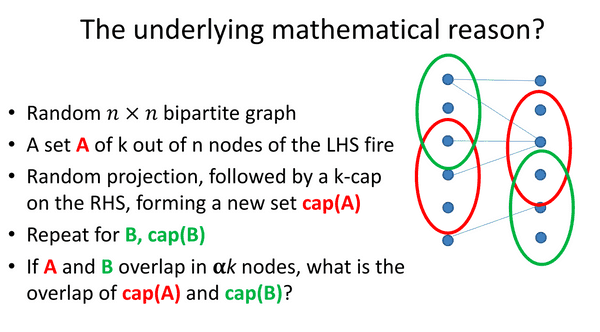
• similarity is preserved by this (random-projection+threshold) procedure; similarity here defined by overlap

  • not really sure what you're gaining though? ¹

• Calculus of the Brain

  • interesting experiment: have a neuron only fire when you see Eiffel tower (vs house or Obama)
    • then super-impose Obama onto Eiffel tower, see below
    • now show Obama, and the neuron will fire (most of the time)
  • what's going on?
    • one way you can think of this is that there's the set of neurons that fire for Eiffel (memory of Eiffel), and similarly for other objects
    • when you see two things together (learning relationships, causality, hierarchy), then what happens is that these two sets of neurons are now connected/merged
    • but in order for this to make sense, the merge operation needs to be a little bit elaborate. basically you have to create the merged version (so like Eiffel+Obama), and perhaps that becomes the channel that connects the two things?
  • this basically gives you something like a calculus on the brain, basically involving set operations on neurons